controlling-pollution: carbon tubes as space elevator

A space elevator is a proposed non-rocket spacelaunch structure (a structure designed to transport material from a celestial body's surface into space). Many elevator variants have been suggested, all of which involve travelling along a fixed structure instead of using rocket powered space launch. The concept most often refers to a cable that reaches from the surface of the Earth on or near theEquator to geostationary orbit (GSO) and a counter-mass outside of the geostationary orbit.

Discussion of a space elevator dates back to 1895 when Konstantin Tsiolkovsky^[1] proposed a free-standing "Tsiolkovsky" tower reaching from the surface of Earth to geostationary orbit. Most recent discussions focus on tensilestructures (specifically, tethers) reaching from geostationary orbit to the ground. This structure would be held in tension between Earth and the counterweight in space like a guitar string held taut. Space elevators have also sometimes been referred to as beanstalks, space bridges, space lifts, space ladders, skyhooks,orbital towers, or orbital elevators.

While some variants of the space elevator concept are technologically feasible, current technology is not capable of manufacturing practical engineering materials that are sufficiently strong and light to build an Earth-based space elevator of the geostationary orbital tether type. Recent conceptualizations for a space elevator are notable in their plans to use carbon nanotube or boron nitride nanotube based materials as the tensile element in the tether design, since the measured strength of microscopic carbon nanotubes appears great enough to make this possible.^[2] Technology as of 1978 could produce elevators for locations in the solar system with weaker gravitational fields, such as the Moonor Mars.^[3]

A further issue is that for human riders on an Earth-based elevator, space radiation due to the Van Allen belts would, if unshielded, give a dose well above permitted levels.^[4] This would not be an issue for non-living cargo, however.

This concept, also called an orbital space elevator, geostationary orbital tether, or a beanstalk, is a subset of the skyhookconcept, and is what people normally think of when the phrase 'space elevator' is used (although there are variants).

Construction would be a large project: the minimum length of an Earth-based space elevator is well over 38,000 km (24,000 mi) long. The tether would have to be built of a material that could endure tremendous stress while also being light-weight, cost-effective, and manufacturable in great quantities. Materials currently available do not meet these requirements, although carbon nanotube technology shows great promise. As with all leading-edge engineering projects, other novel engineering problems would also have to be solved to make a space elevator practical, and there are problems regarding feasibility that have yet to be addressed

Physics of space elevators

[edit]Apparent gravitational field

The space elevator cable rotates along with the rotation of the Earth. Objects fastened to the cable will experience upward centrifugal force that opposes some, all, or more than the downward gravitational force at that point. Along the length of the cable, the actual(downward) gravity minus the (upward) centrifugal force is called the apparent gravitational field.

The apparent gravitational field can be computed this way:

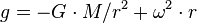$g = -G \cdot M/r^2 + \omega^2 \cdot r$ , where

g is the acceleration along the radius (m s^-2),

G is the gravitational constant (m³ s^-2 kg^-1)

M is the mass of the Earth (kg)

r is the distance from that point to Earth's center (m),

ω is Earth's rotation speed (radians/s).

Near the earth's surface the acceleration g₀ at radius r₀ is given by:

$g_0 = G \cdot M/r_0^2$ (the other term is negligible), so that:

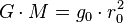$G \cdot M= g_0 \cdot r_0^2$ , which gives the $G \cdot M$ constant given the ground acceleration and planet radius.

At some point r₁ above the equator line, the two terms (gravity and centrifugal force) equal each other, the tether then carries no weight. This occurs at the level of the stationary orbit:

$r_1 = (g_0 \cdot r_0^2/\omega^2)^{1/3}$ which is to say $G \cdot M/r_1^2 = \omega^2 \cdot r_1$ , which gives the value of r₁.

The same holds true for any planet or satellite.

Seen from a geosynchronous station, any object dropped off the tether from a point closer to Earth will initially accelerate downward. If dropped from any point above a geosynchronous station, the object would initially accelerate up toward space. If a long cable is dropped "down" (toward Earth), it must be properly balanced by balancing mass being dropped "up" (away from Earth) for the whole system to remain on the geosynchronous orbit. Some designs imagine the balancing mass being another cable (with counterweight) extending upward, other designs elevate the spool itself as the main cable is payed out. When the lower end of the cable is so long as to reach the Earth, it can be anchored at some place. Once anchored, if more mass is added at the remote end, it will add a tension to the whole cable, which can then be used as an elevator cable.

[edit]Cable section

The main technical problem is the long cable's own weight. The cable material combined with its design must be strong enough to hold up 35000 km (22,000 mi) of itself. The primary design factor other than the material is the taper ratio, that is, the ratio and taper rate of the cross sectional area of the cable as it goes from GEO to ground level. The solution is to build it in such a way that at any given point, its cross section area is proportional to the force it has to withstand, that is, the section must follow the following differential equation:

$\sigma \cdot dS = g \cdot \rho \cdot S \cdot dr$ , where

g is the acceleration along the radius (m·s⁻²),

S is the cross-area of the cable at any given point r, (m²) and dS its variation (m² as well),

ρ is the density of the material used for the cable (kg·m⁻³).

σ is the stress a given area can bear without splitting (N·m⁻²=kg·m⁻¹·s⁻²), its elastic limit

The value of g is given by the first equation, which yields:

$\Delta\left[ \ln (S)\right]{}_{r_1}^{r_0} = \rho/\sigma \cdot \Delta\left[ G \cdot M/r + w^2 \cdot r^2/2 \right]{}_{r_1}^{r_0}$ ,

the variation being taken between r₁ (geostationary) and r₀ (ground).

It turns out that between these two points, this quantity can be expressed simply as: $\Delta\left[ \ln (S)\right] = \rho/\sigma \cdot g_0 \cdot r_0 \cdot ( 1 + x/2 - 3/2 \cdot x^{1/3} )$ , or

$S_0 = S_1.e^{\rho/\sigma \cdot g_0 \cdot r_0 \cdot ( 1 + x/2 - 3/2 \cdot x^{1/3} )}$

where $x = \omega^2 \cdot r_0/g_0$ is the ratio between the centrifuge force on the equator and the gravitational force.

Thus, the factor with the main influence is g₀ r₀, the combination of the planet's radius and its surface gravity. The rotational speed is slightly influential, but only as a corrective factor. For Earth, it reduces the strength needed by about one third.

[edit]Cable material

The second technical problem is that the g₀ r₀ factor is quite large. Since its influence on the maximal cross-section is exponential, one needs to find materials where σ will be large enough to cancel our gravity. On Earth, we have:

$g_0 \cdot r_0 = 62.5 \cdot 10^6~m^2s^{-2}$ (or Joules per kg)

$\rho \approx 3 \cdot 10^3~kg~m^{-3}$ for most solid materials, so that σ needs to be:

$\sigma \approx 300 \cdot 10^9~kg~m^{-1}s^{-2}$

This corresponds to a cable capable of sustaining 30 tons with a cross-section of one square millimeter, under Earth's gravity.

The free breaking length can be used to compare materials: it is the length of a cylindrical cable at which it will split under its own weight (under constant gravity). For a given material, that length is σ/ρ/g₀. The free breaking length needed is given by the equation

$\Delta\left[ \ln (S)\right] = \rho/\sigma \cdot g_0 \cdot r_0 \cdot ( 1 + x/2 - 3/2 \cdot x^{1/3} )$ , where $x = w^2 \cdot r_0/g_0$

If one does not take into account the x factor (which reduces the strength needed by about 30%), this equation also says that the section ratio equals e (exponential one) when:

$\sigma = \rho \cdot r_0 \cdot g_0$

In other words, the free breaking length is approximately equal to the planet's radius under its own gravity. Since the section ratio varies exponentially, the free breaking length must be at least of that order of magnitude. If the material is only ten times less resilient, the section needed at a geosynchronous orbit will be e¹⁰ times the ground section, which is more than a hundredfold in diameter, which is practically impossible.

[edit]Structure

One concept for the space elevator has it tethered to a mobile seagoing platform.

The centrifugal force of earth's rotation is the main principle behind the elevator. As the earth rotates, the centrifugal force tends to align the nanotube in a stretched manner. There are a variety of tether designs. Almost every design includes a base station, a cable, climbers, and a counterweight.

[edit]Base station

The base station designs typically fall into two categories—mobile and stationary. Mobile stations are typically large oceangoing vessels.^[28] Stationary platforms would generally be located in high-altitude locations, such as on top of mountains, or even potentially on high towers.^[6]

Mobile platforms have the advantage of being able to maneuver to avoid high winds, storms, and space debris. While stationary platforms don't have these advantages, they typically would have access to cheaper and more reliable power sources, and require a shorter cable. While the decrease in cable length may seem minimal (no more than a few kilometers), the cable thickness could be reduced over its entire length, significantly reducing the total weight.

[edit]Cable

Carbon nanotubes are one of the candidates for a cable material

A space elevator cable must carry its own weight as well as the (smaller) weight of climbers. The required strength of the cable will vary along its length, since at various points it has to carry the weight of the cable below, or provide a centripetal force to retain the cable and counterweight above. In a 1998 report,^[29] NASA researchers noted that "maximum stress [sic] [on a space elevator cable] is at geosynchronous altitude so the cable must be thickest there and taper exponentially as it approaches Earth. Any potential material may be characterized by the taper factor – the ratio between the cable's radius at geosynchronous altitude and at the Earth's surface."

The cable must be made of a material with a large tensile strength/mass ratio. For example, the Edwards space elevator design assumes a cable material with a specific strength of at least 100,000 kN/(kg/m).^[30] This value takes into consideration the entire weight of the space elevator. A space elevator would need a material capable of sustaining a length of 4,960 kilometers (3082 mi) of its own weight at sea level to reach a geostationary altitude of 36,000 km (22,300 mi) without tapering and without breaking.^[31] Therefore, a material with very high strength and lightness is needed.

For comparison, metals like titanium, steel or aluminium alloys have breaking lengths of only 20–30 km. Modern fibre materials (which tend to achieve greater strength because the microscopic or crystal structure is aligned with the axis of the material and has fewer defects) such as kevlar, fibreglass and carbon/graphite fibre have breaking lengths of 100–400 km. Quartz fibers have an advantage that they can be drawn to a length of hundreds of kilometers ^[32] even with the present-day technology. Nanoengineered materials such ascarbon nanotubes and, more recently discovered, graphene ribbons (perfect two-dimensional sheets of carbon) are expected to have breaking lengths of 5000–6000 km at sea level, and also are able to conduct electrical power.

Carbon is such a good candidate material (for high specific strength) because, as only the 6th element in the periodic table, it has very few of the nucleons which contribute most of the dead weight of any material (whereas most of the interatomic bonding forces are contributed by only the outer few electrons); the challenge now remains to extend to macroscopic sizes the production of such material that are still perfect on the microscopic scale (as microscopic defects are most responsible for material weakness). The current (2009) carbon nanotube technology allows growing tubes up to a few tens of centimeters only^[33].

A seagoing anchor station would incidentally act as a deep-water seaport.

[edit]Climbers

A conceptual drawing of a space elevator climbing through the clouds.

A space elevator cannot be an elevator in the typical sense (with moving cables) due to the need for the cable to be significantly wider at the center than the tips. While various designs employing moving cables have been proposed, most cable designs call for the "elevator" to climb up a stationary cable.

Climbers cover a wide range of designs. On elevator designs whose cables are planar ribbons, most propose to use pairs of rollers to hold the cable with friction.

Climbers must be paced at optimal timings so as to minimize cable stress and oscillations and to maximize throughput. Lighter climbers can be sent up more often, with several going up at the same time. This increases throughput somewhat, but lowers the mass of each individual payload.^{[citation needed]}

As the car climbs, the elevator takes on a 1 degree lean, due to the top of the elevator traveling faster than the bottom around the Earth (Coriolis force). This diagram is not to scale.

The horizontal speed of each part of the cable increases with altitude, proportional to distance from the center of the Earth, reaching orbital velocity at geostationary orbit. Therefore as a payload is lifted up a space elevator, it needs to gain not only altitude butangular momentum (horizontal speed) as well. This angular momentum is taken from the Earth's own rotation. As the climber ascends it is initially moving slightly more slowly than the cable that it moves onto (Coriolis force) and thus the climber "drags" on the cable.

The overall effect of the centrifugal force acting on the cable causes it to constantly try to return to the energetically favourable vertical orientation, so after an object has been lifted on the cable the counterweight will swing back towards the vertical like an inverted pendulum^{[citation needed]}. Provided that the space elevator is designed so that the center of weight always stays above geostationary orbit^[34] for the maximum climb speed of the climbers, the elevator cannot fall over. Lift and descent operations must be carefully planned so as to keep the pendulum-like motion of the counterweight around the tether point under control.^[35]

By the time the payload has reached GEO the angular momentum (horizontal speed) is enough that the payload is in orbit.

The opposite process would occur for payloads descending the elevator, tilting the cable eastwards and insignificantly increasing Earth's rotation speed.

It has also been proposed to use a second cable attached to a platform to lift payload up the main cable, since the lifting device would not have to deal with its own weight against Earth's gravity. Out of the many proposed theories, powering any lifting device also continues to present a challenge.

Another design constraint will be the ascending speed of the climber. As geosynchronous orbit is at 35,786 km (22,236 mi). Assuming the climber can reach the speed of a very fast car or train of 300 km/h (180 mph) it will take 5 days to climb to geosynchronous orbit.

[edit]Powering climbers

Both power and energy are significant issues for climbers—the climbers need to gain a large amount of potential energy as quickly as possible to clear the cable for the next payload.

All proposals to get that energy to the climber fall into 3 categories:^{[citation needed]}

transfer the energy to the climber through wireless energy transfer while it is climbing
transfer the energy to the climber through some material structure while it is climbing
store the energy in the climber before it starts—this requires an extremely highspecific energy. Nuclear energy and solar power have been proposed, but generating enough energy to reach the top of the elevator in any reasonable time without weighing too much is not feasible.^[36]

The proposed method is laser power beaming, using megawatt powered free electron or solid state lasers in combination with adaptive mirrors approximately 10 m (33 ft) wide and a photovoltaic array on the climber tuned to the laser frequency for efficiency.^[28] A major obstacle for any climber design is the dissipation of the substantial amount of waste heat generated due to the less than perfect efficiency of any of the power methods.

Yoshio Aoki, a professor of precision machinery engineering at Nihon University and director of the Japan Space Elevator Association, suggested including a second cable and using the conductivity of carbon nanotubes to provide power.^[26]

Various mechanical means of applying power have also been proposed; such as moving, looped or vibrating cables.^{[citation needed]}

[edit]Counterweight

Several solutions have been proposed to act as a counterweight:

a heavy, captured asteroid;^[5]
a space dock, space station or spaceport positioned past geostationary orbit; or
an extension of the cable itself far beyond geostationary orbit.

The third idea has gained more support in recent years^{[year needed]} due to the relative simplicity of the task and the fact that a payload that went to the end of the counterweight-cable would acquire considerable velocity relative to the Earth, allowing it to be launched into interplanetary space.

Additionally, Brad Edwards has proposed that initially elevators would be up-only, and that the elevator cars that are used to thicken the cable could simply be parked at the top of the cable and act as a counterweight.

[edit]Alternative concepts

Many different types of structures for accessing space have been suggested. As of 2004, concepts using geostationary tethers seem to be the only space elevator concept that is the subject of active research and commercial interest in space.^[37]

The original concept envisioned by Tsiolkovsky was a compression structure, a concept similar to an aerial mast. While such structures might reach the agreed altitude for space (100 km—62 mi), they are unlikely to reach geostationary orbit (35,786 km—22,236 mi). The concept of a Tsiolkovsky tower combined with a classic space elevator cable has been suggested.^[6] Other alternatives to a space elevator include an orbital ring, a pneumatic space tower, ^[38] a space fountain, a launch loop, a Skyhook, a space tether, and a space hoist.

[edit]Launching into deep space

The velocities that might be attained at the end of Pearson's 144,000 km (90,000 mi) cable can be determined. The tangential velocity is 10.93 kilometers per second (6.79 mi/s), which is more than enough to escape Earth's gravitational field and send probes at least as far out as Jupiter. Once at Jupiter a gravitational assist maneuver permits solar escape velocity to be reached.^[39]

[edit]Extraterrestrial elevators

A space elevator could also be constructed on other planets, asteroids and moons.

A Martian tether could be much shorter than one on Earth. Mars' surface gravity is 38% of Earth's, while it rotates around its axis in about the same time as Earth.^[40] Because of this, Martian areostationary orbit is much closer to the surface, and hence the elevator would be much shorter. Current materials are already sufficiently strong to construct such an elevator.^[41] However, building a Martian elevator would be complicated by the Martian moon Phobos, which is in a low orbit and intersects the Equator regularly (twice every orbital period of 11 h 6 min).

A lunar space elevator can possibly be built with currently available technology about 50,000 kilometers (31,000 miles) long extending through the Earth-Moon L1 point from an anchor point near the center of the visible part of Earth's moon.^[42]

On the far side of the moon, a lunar space elevator would need to be very long (more than twice the length of an Earth elevator) but due to the low gravity of the Moon, can be made of existing engineering materials.^[42]

Rapidly spinning asteroids or moons could use cables to eject materials to convenient points, such as Earth orbits;^{[citation needed]} or conversely, to eject materials to send the bulk of the mass of the asteroid or moon to Earth orbit or a Lagrangian point. Freeman Dyson, a physicist and mathematician, has suggested^{[citation needed]} using such smaller systems as power generators at points distant from the Sun where solar power is uneconomical. For the purpose of mass ejection, it is not necessary to rely on the asteroid or moon to be rapidly spinning. Instead of attaching the tether to the equator of a rotating body, it can be attached to a rotating hub on the surface. This was suggested in 1980 as a "Rotary Rocket" by Pearson^[43] and described very succinctly on the Island One website as a "Tapered Sling".^[44]

controlling-pollution

Saturday, January 22, 2011

carbon tubes as space elevator